2.1.1 进位技术制及相互转换

r进制计数法

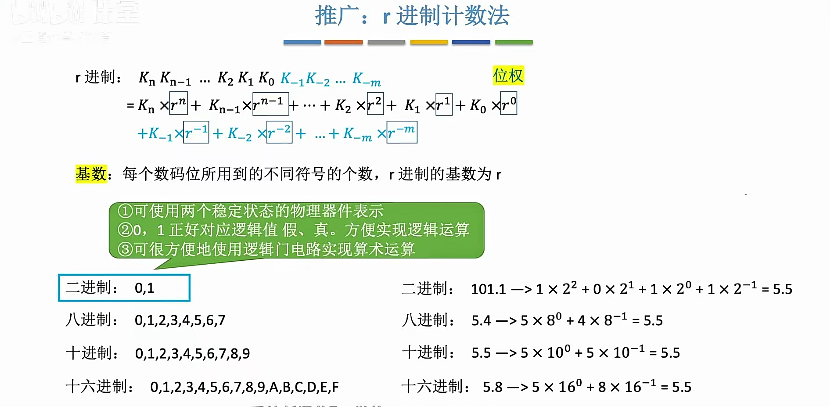
任意进制->十进制

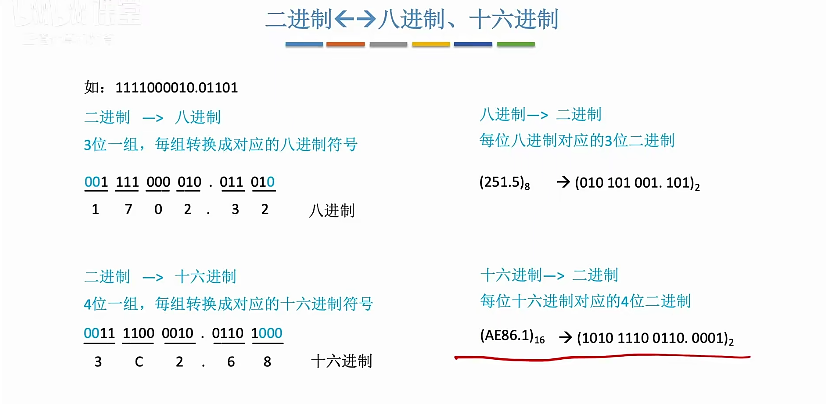
二进制<->八进制、十六进制

各种进制的常见书写方式

十进制->二进制

需要分为整数部分和小数部分，整数部分使用除基取余法，小数部分使用乘基取整法。

2105十进制->二进制（拼凑法）

真值和机器数

知识回顾

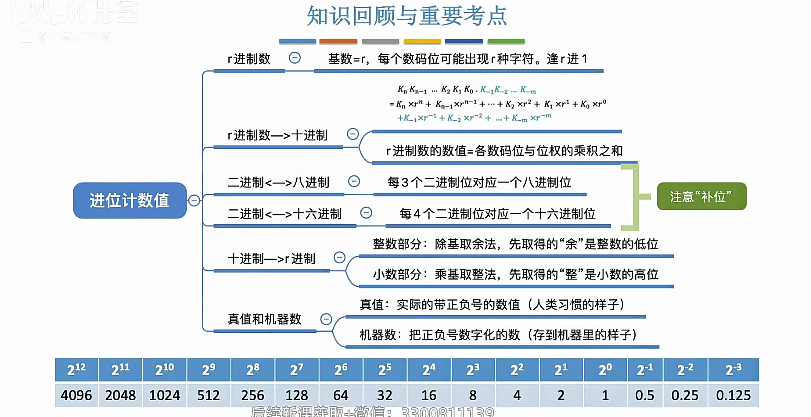
2.1.3 定点数的编码表示

计算机的运算器中只有加法器，所以要将减法转换为加法计算

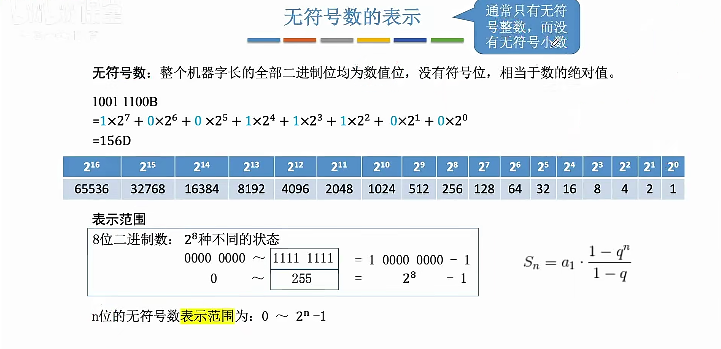
无符号数的表示

原码

原码表示定点小数

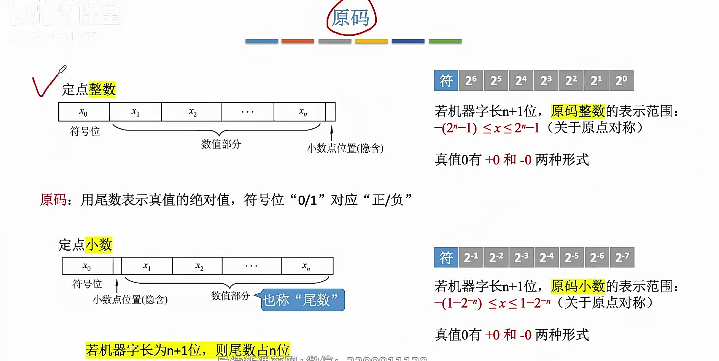
原码表示定点整数

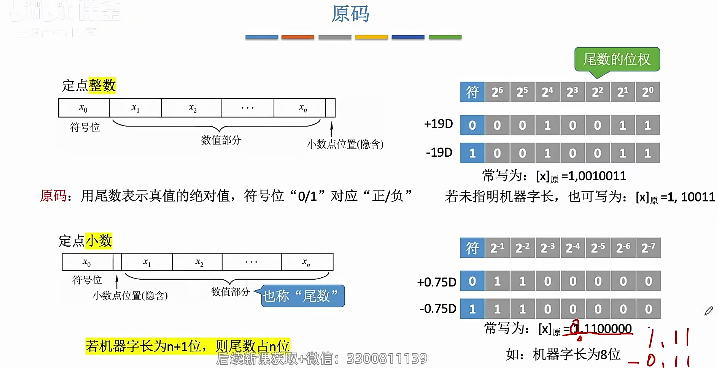
反码

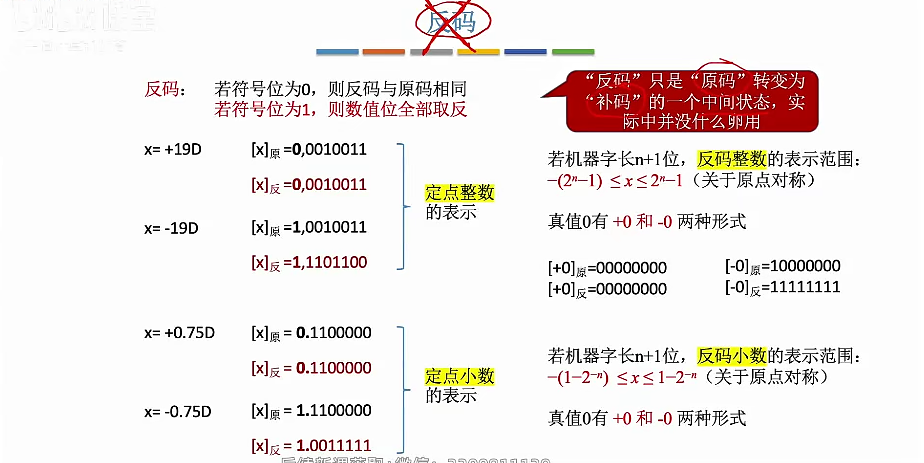
补码

在反码的基础上+1

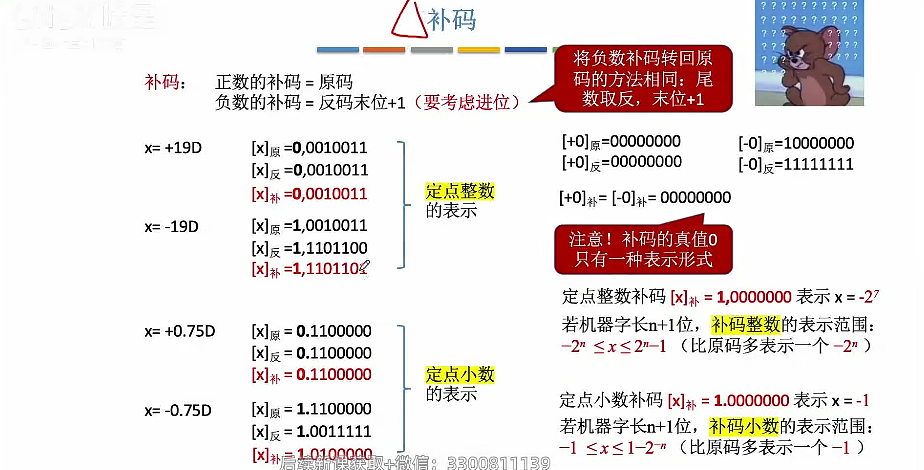
移码

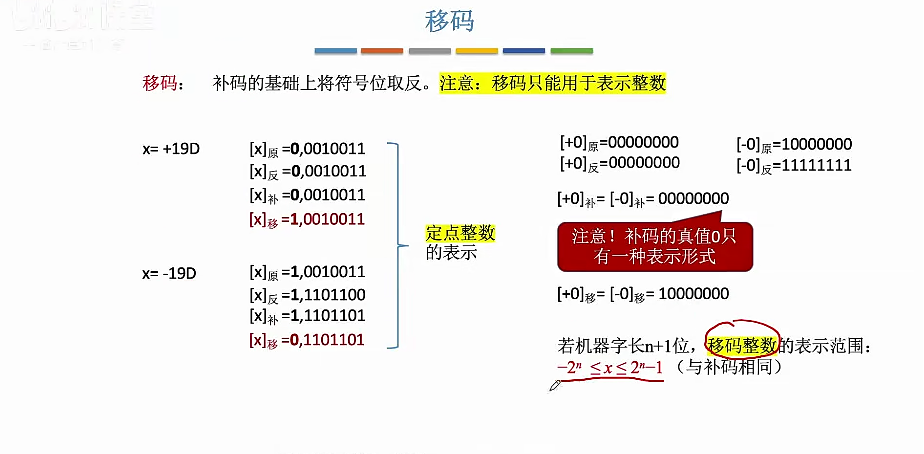
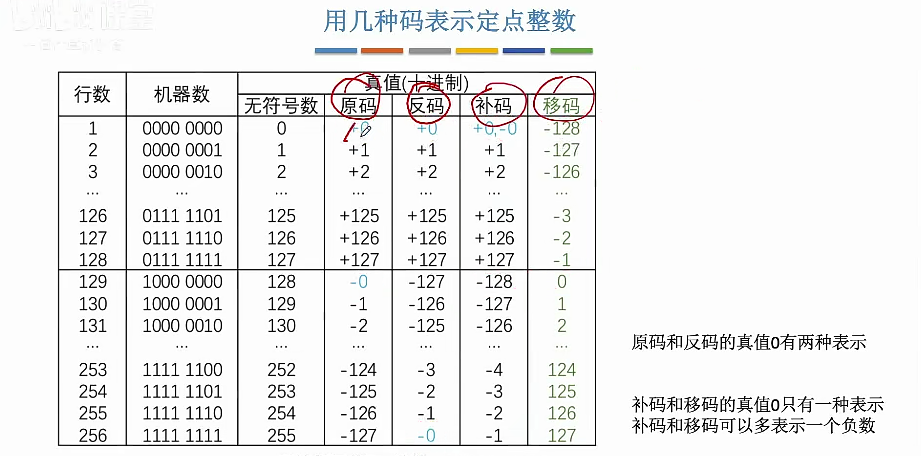
例子

原码

x = 14(D)
原码：0000 1110

x = -21(D)
原码：1001 0101

原码->反码

# 正数：补码=反码=原码
# 负数：反码=标志位不变，其他取反

x = 14(D)
原码：0000 1110
反码：0000 1110

x=-21(D)
原码：1001 0101
反码：1110 1010

原码->补码

# 正数：补码=反码=原码
# 负数：补码=原码->反码->+1

x = 14(D)
原码：0000 1110
反码：0000 1110
补码：0000 1110

x=-21(D)
原码：1001 0101
反码：1110 1010
补码：1110 1011

计算机的计算方式

例子1：计算 14+(-21)

1. 补码+补码

0000 1110
1110 1011
----------
1111 1001  = -7（补）

2. 补码->反码
# 正数：补码=反码=原码
# 负数：反码=补码->-1

1111 1001 = -7（补）
1111 1000 = -7（反）

3. 反码->原码
# 正数：补码=反码=原码
# 负数：反码=标志位不变，其他取反

1111 1001 = -7（反）
1000 0111 = -7（原）

例子2：计算 14-(-21) = 14 + 21

1. 补码+补码

0000 1110
0001 0101
----------
1110 0011  = 35（补）